LeetCode-数据结构与算法简介,入门及攻略
数据结构与算法

数据结构是程序的骨架,而算法则是程序的灵魂。
数据结构
数据结构(Data Structure):带有结构特性的数据元素的集合。
Microsoft Word 这个单词,然后很快的定位到 「Microsoft Word」这个应用程序的文件信息,从而从文件信息中找到对应的磁盘位置。1. 数据的逻辑结构
逻辑结构(Logical Structure):数据元素之间的相互关系。
- 集合结构
集合结构:数据元素同属于一个集合,除此之外无其他关系。

- 线性结构
线性结构:数据元素之间是「一对一」关系。

- 树形结构
树形结构:数据元素之间是「一对多」的层次关系。

- 图形结构
图形结构:数据元素之间是「多对多」的关系。

2. 数据的物理结构
物理结构(Physical Structure):数据的逻辑结构在计算机中的存储方式。
- 顺序存储结构
顺序存储结构(Sequential Storage Structure):将数据元素存放在一片地址连续的存储单元里,数据元素之间的逻辑关系通过数据元素的存储地址来直接反映。

- 链式存储结构
链式存储结构(Linked Storage Structure):将数据元素存放在任意的存储单元里,存储单元可以连续,也可以不连续。

算法
算法(Algorithm):解决特定问题求解步骤的准确而完整的描述,在计算机中表现为一系列指令的集合,算法代表着用系统的方法描述解决问题的策略机制。
- 示例 1:
问题描述:
从上海到北京,应该怎么去?
解决方法:
- 选择坐飞机,坐飞机用的时间最少,但费用最高。
- 选择坐长途汽车,坐长途汽车费用低,但花费时间长。
- 选择坐高铁或火车,花费时间不算太长,价格也不算太贵。
- 示例2:
问题描述:
如何计算 1+2+3+…+100 的值?
解决方法:
用计算器从 1 开始,不断向右依次加上 2,再加上 3,…,依次加到 100,得出结果为 5050。
根据高斯求和公式:和 = (首项 + 末项) * 项数 / 2,直接算出结果为:(1+100)∗100/2=5050。
- 示例 3:
问题描述:
- 如何对一个 n 个整数构成的数组进行升序排序?
解决方法:
- 使用冒泡排序对 n 个整数构成的数组进行升序排序。
- 选择插入排序、归并排序、快速排序等等其他排序算法对 n 个整数构成的数组进行升序排序。
1. 算法的基本特性
- 输入:对于待解决的问题,都要以某种方式交给对应的算法。在算法开始之前最初赋给算法的参数称为输入。一个算法可以有多个输入,也可以没有输入。
- 输出:算法是为了解决问题存在的,最终总需要返回一个结果。所以至少需要一个或多个参数作为算法的输出。
- 有穷性:算法必须在有限的步骤内结束,并且应该在一个可接受的时间内完成。
- 确定性:组成算法的每一条指令必须有着清晰明确的含义,不能令读者在理解时产生二义性或者多义性。就是说,算法的每一个步骤都必须准确定义而无歧义。
- 可行性:算法的每一步操作必须具有可执行性,在当前环境条件下可以通过有限次运算实现。也就是说,每一步都能通过执行有限次数完成,并且可以转换为程序在计算机上运行并得到正确的结果。
2. 算法追求的目标
- 所需运行时间更少(时间复杂度更低)
- 占用内存空间更小(空间复杂度更低)
- 正确性:正确性是指算法能够满足具体问题的需求,程序运行正常,无语法错误,能够通过典型的软件测试,达到预期的需求。
- 可读性:可读性指的是算法遵循标识符命名规则,简洁易懂,注释语句恰当,方便自己和他人阅读,便于后期修改和调试。
- 健壮性:健壮性指的是算法对非法数据以及操作有较好的反应和处理。
总结
- 逻辑结构可分为:集合结构、线性结构、树形结构、图形结构。
- 物理结构可分为:顺序存储结构、链式存储结构。
- 输入
- 输出
- 有穷性
- 确定性
- 可行性
- 正确性
- 可读性
- 健壮性
- 所需运行时间更少(时间复杂度更低)
- 占用内存空间更小(空间复杂度更低)
参考资料
- 【文章】数据结构与算法 · 看云
- 【书籍】大话数据结构——程杰 著
- 【书籍】趣学算法——陈小玉 著
- 【书籍】计算机程序设计艺术(第一卷)基本算法(第三版)——苏运霖 译
- 【书籍】算法艺术与信息学竞赛——刘汝佳、黄亮 著
- datawhale leetcode-notes
算法复杂度
算法复杂度简介
算法复杂度(Algorithm complexity):在问题的输入规模为n的条件下,程序的时间使用情况和空间使用情况。
- 事后统计:将两个算法各编写一个可执行程序,交给计算机执行,记录下各自的运行时间和占用存储空间的实际大小,从中挑选出最好的算法。
- 预先估算:在算法设计出来之后,根据算法中包含的步骤,估算出算法的运行时间和占用空间。比较两个算法的估算值,从中挑选出最好的算法。
n扩大时,时间开销、空间开销的增长情况。- 排序算法中:n 表示需要排序的元素数量。
- 查找算法中:n 表示查找范围内的元素总数:比如数组大小、二维矩阵大小、字符串长度、二叉树节点数、图的节点数、图的边界点等。
- 二进制计算相关算法中:n 表示二进制的展开宽度。
时间复杂度
1. 时间复杂度简介
时间复杂度(Time Complexity):在问题的输入规模为 n 的条件下,算法运行所需要花费的时间,可以记作为 $T(n)$。
- 基本操作 :算法执行中的每一条语句。每一次基本操作都可在常数时间内完成。
def algorithm(n):
fact = 1
for i in range(1, n + 1):
fact *= i
return fact2. 渐进符号
渐进符号(Asymptotic Symbol):专门用来刻画函数的增长速度的。简单来说,渐进符号只保留了 最高阶幂,忽略了一个函数中增长较慢的部分,比如 低阶幂、系数、常量。因为当问题规模变的很大时,这几部分并不能左右增长趋势,所以可以忽略掉。
- $ Θ$ 渐进紧确界符号
- $O$ 渐进上界符号
- $Ω$ 渐进下界符号
3. 时间复杂度计算
- 找出算法中的基本操作(基本语句):算法中执行次数最多的语句就是基本语句,通常是最内层循环的循环体部分
- 计算基本语句执行次数的数量级:只需要计算基本语句执行次数的数量级,即保证函数中的最高次幂正确即可。像最高次幂的系数和低次幂可以忽略
- 用大 O 表示法表示时间复杂度:将上一步中计算的数量级放入 O 渐进上界符号中
- 加法原则:总的时间复杂度等于量级最大的基本语句的时间复杂度
- 乘法原则:循环嵌套代码的复杂度等于嵌套内外基本语句的时间复杂度乘积
常数$O(1)$
def algorithm(n):
a = 1
b = 2
res = a * b + n
return res线性$O(n)$
def algorithm(n):
sum = 0
for i in range(n):
sum += 1
return sum平方$O(n^2)$
def algorithm(n):
res = 0
for i in range(n):
for j in range(n):
res += 1
return res阶乘$O(n!)$
def permutations(arr, start, end):
if start == end:
print(arr)
return
for i in range(start, end):
arr[i], arr[start] = arr[start], arr[i]
permutations(arr, start + 1, end)
arr[i], arr[start] = arr[start], arr[i]对数$O(log n)$
def algorithm(n):
cnt = 1
while cnt < n:
cnt *= 2
return cnt线性对数$O(n*logn)$
def algorithm(n):
cnt = 1
res = 0
while cnt < n:
cnt *= 2
for i in range(n):
res += 1
return res常见时间复杂度关系
4. 最佳、最坏、平均时间复杂度
- 最佳时间复杂度:每个输入规模下用时最短的输入所对应的时间复杂度
- 最坏时间复杂度:每个输入规模下用时最长的输入所对应的时间复杂度
- 平均时间复杂度:每个输入规模下所有可能的输入所对应的平均用时复杂度(随机输入下期望用时的复杂度)
空间复杂度
1. 空间复杂度简介
空间复杂度(Space Complexity):在问题的输入规模为 n 的条件下,算法所占用的空间大小,可以记作为 $O(n)$。一般将 算法的辅助空间 作为衡量空间复杂度的标准。
2. 空间复杂度计算
常数$O(1)$
def algorithm(n):
a = 1
b = 2
res = a * b + n
return resa、b、res 这 3 个局部变量,其所占空间大小为常数阶,并不会随着问题规模 n 的在增大而增大,所以该算法的空间复杂度为 $O(1)$。线性$O(n)$
def algorithm(n):
if n <= 0:
return 1
return n * algorithm(n - 1)常见的复杂度关系
算法复杂度总结
-
常见的时间复杂度有:$O(1)、O(logn)、O(n)、O(n×logn)、O(n^2)、O(n^3)、O(2^n)、O(n!)$。
-
常见的空间复杂度有:$O(1)、O(logn)、O(n)、O(n^2)$。
参考资料
- 【书籍】数据结构(C++ 语言版)- 邓俊辉 著
- 【书籍】算法导论 第三版(中文版)- 殷建平等 译
- 【书籍】算法艺术与信息学竞赛 - 刘汝佳、黄亮 著
- 【书籍】数据结构(C 语言版)- 严蔚敏 著
- 【书籍】趣学算法 - 陈小玉 著
- 【文章】复杂度分析 - 数据结构与算法之美 王争
- 【文章】算法复杂度(时间复杂度+空间复杂度)
- 【文章】算法基础 - 复杂度 - OI Wiki
- 【文章】图解算法数据结构 - 算法复杂度 - LeetBook - 力扣
- datawhale leetcode
LeetCode入门及攻略
LeetCode是什么
LeetCode新手入门
1.LeetCode注册
- 打开 LeetCode 中文主页,链接:力扣(LeetCode)官网。
- 输入手机号,获取验证码。
- 输入验证码之后,点击「登录 / 注册」,就注册好了。
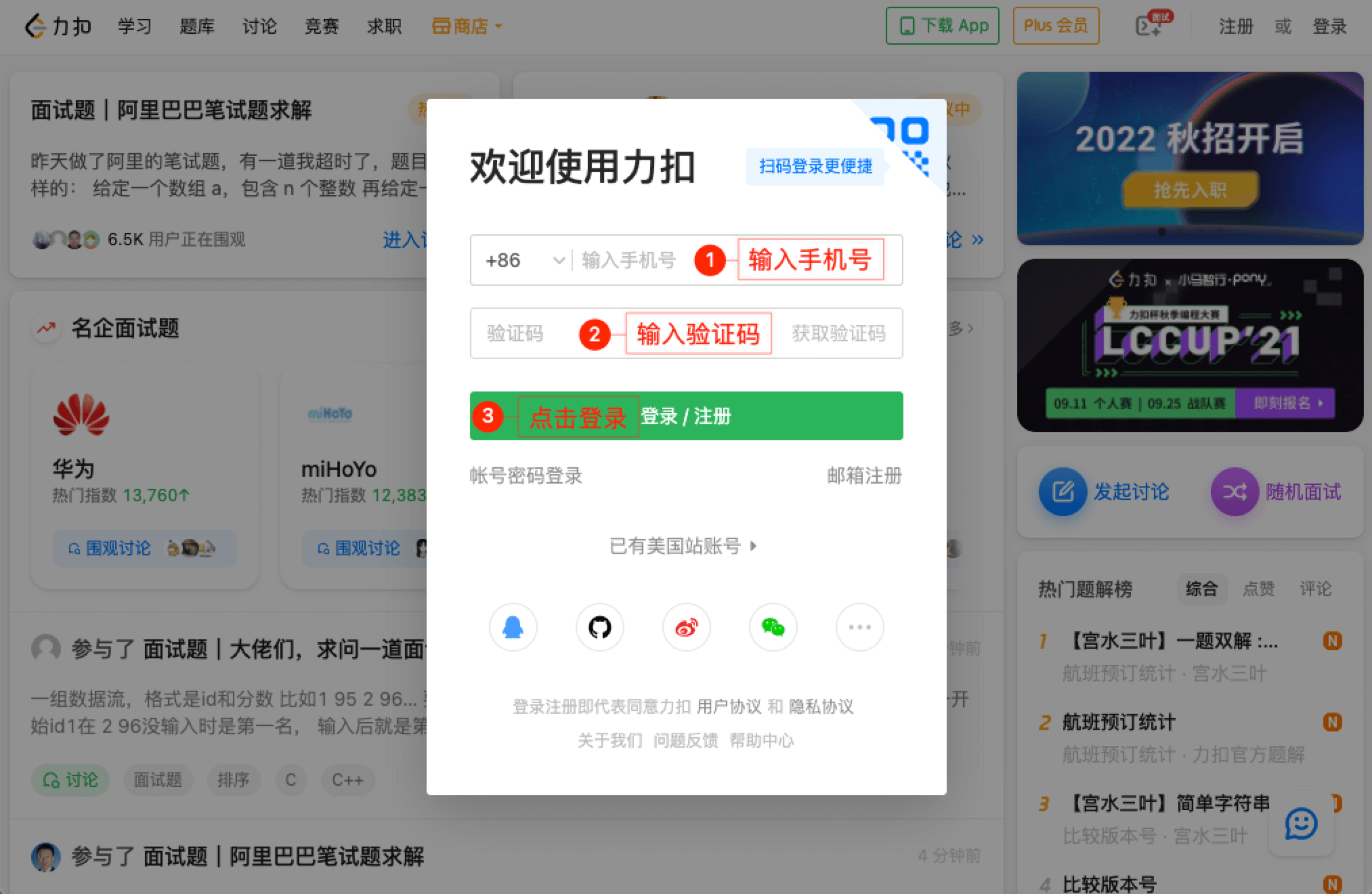
2. LeetCode题库
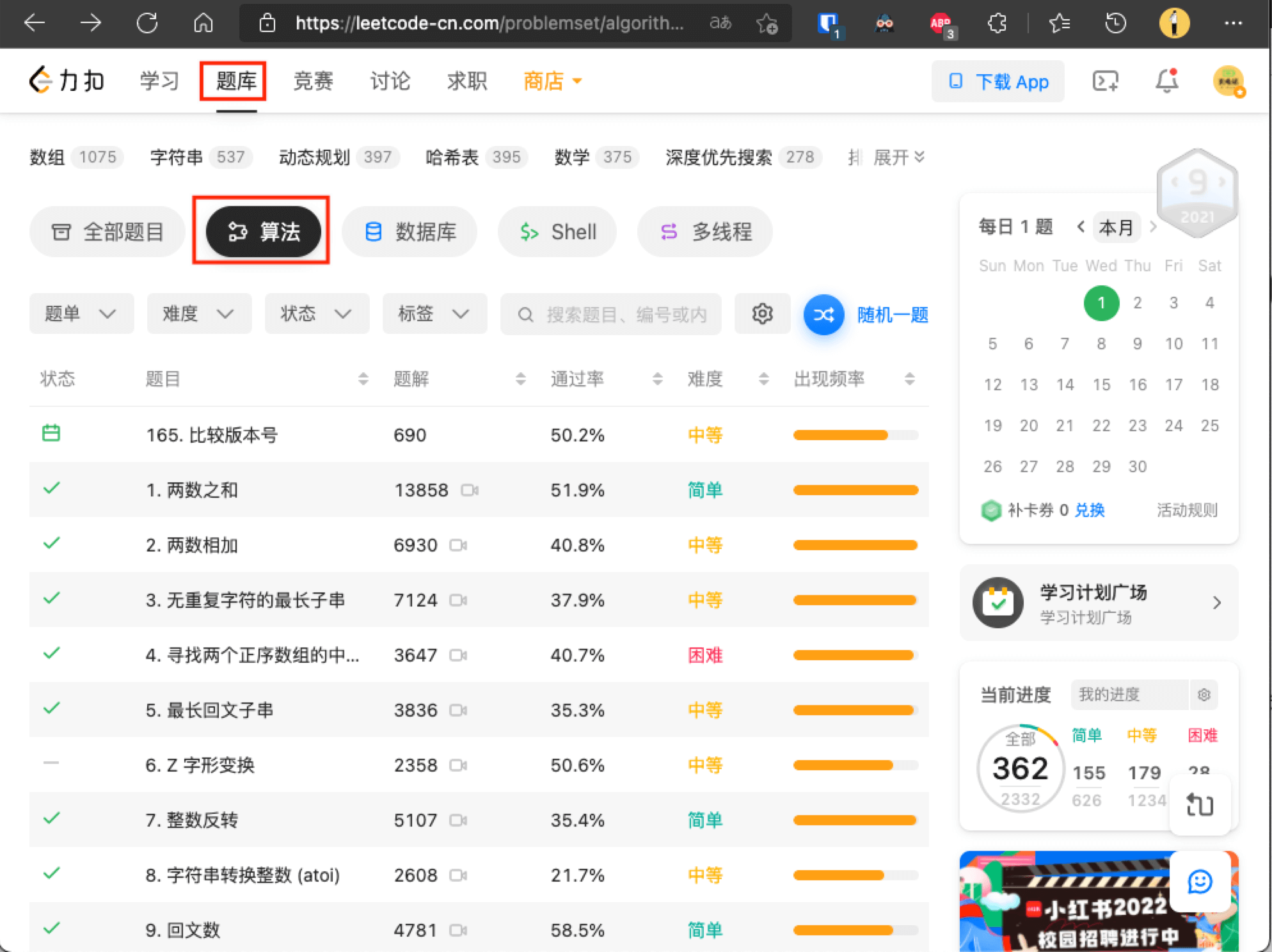
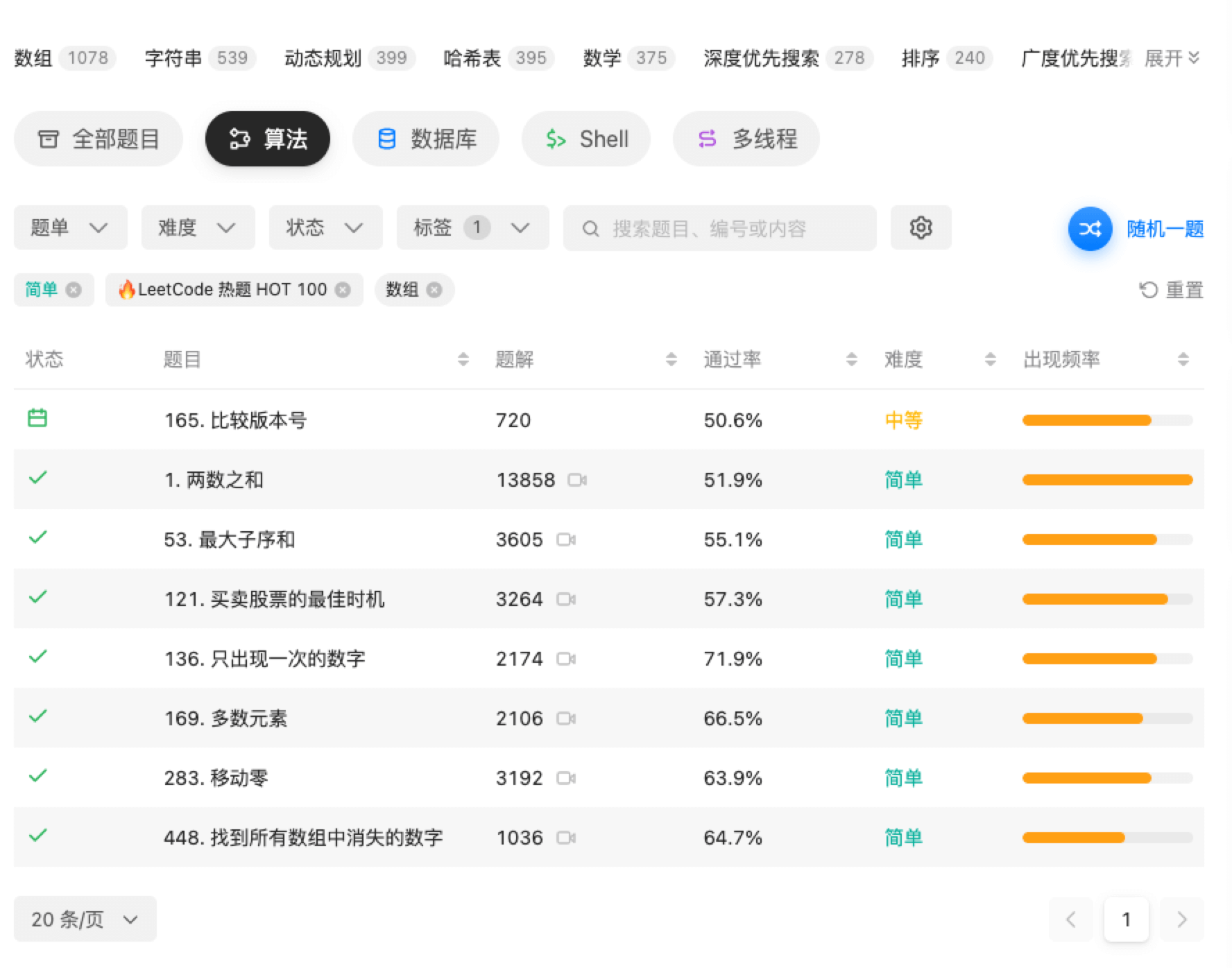
题目标签

题目列表
当前进度
题目详情
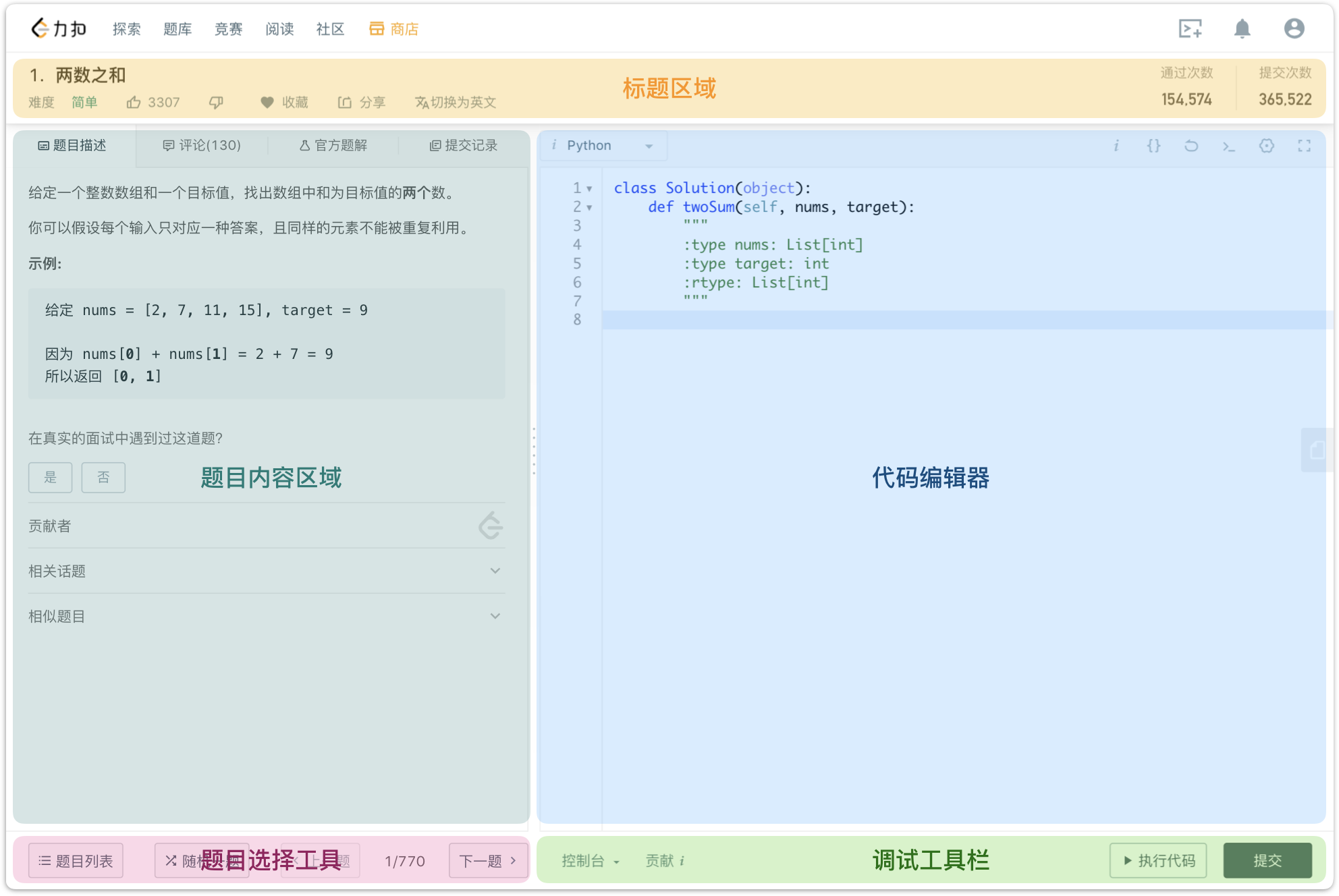
3. LeetCode刷题语言
人生苦短,我用 Python。
4. LeetCode刷题流程

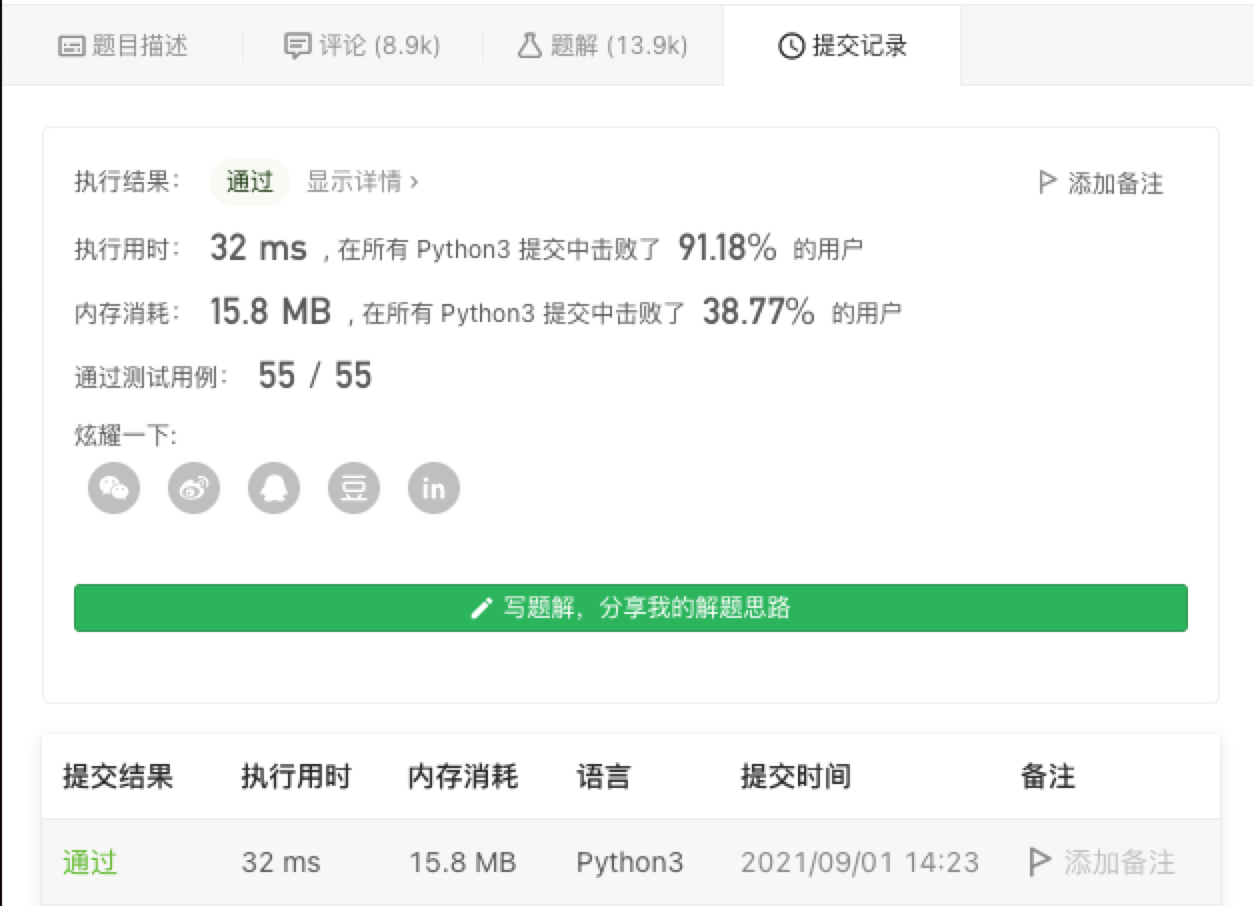
- 在 LeetCode 题库中选择一道自己想要解决的题目。
- 查看题目左侧的题目描述,理解题目要求。
- 思考解决思路,并在右侧代码编辑区域实现对应的方法,并返回题目要求的结果。
- 如果实在想不出解决思路,可以查看题目相关的题解,努力理解他人的解题思路和代码。
- 点击「执行代码」按钮测试结果。
- 如果输出结果与预期结果不符,则回到第 3 步重新思考解决思路,并改写代码。
- 如果输出结果与预期符合,则点击「提交」按钮。
- 如果执行结果显示「编译出错」、「解答错误」、「执行出错」、「超出时间限制」、「超出内存限制」等情况,则需要回到第 3 步重新思考解决思路,或者思考特殊数据,并改写代码。
- 如果执行结果显示「通过」,恭喜你通过了这道题目。
5. LeetCode第一题
题目链接
题目大意
- $2≤nums.length≤10^4$
- $−10^9≤nums[i]≤10^9$
- $−10^9≤target≤10^9$
- 只会存在一个有效答案
- 示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] - 示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]解题思路
思路1:枚举算法
-
使用两重循环枚举数组中每一个数 $nums[i]$、$nums[j]$,判断所有的$nums[i]+nums[j]$ 是否等于 $target$
-
如果出现$nums[i]+nums[j]==target$ ,则说明数组中存在和为$target$ 的两个整数,将两个整数的下标 $i$、$j$ 输出即可
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
for i in range(len(nums)):
for j in range(i + 1, len(nums)):
if i != j and nums[i] + nums[j] == target:
return [i, j]
return []- 时间复杂度:$(n^2)$,其中 n 是数组 $nums$ 的元素数量。
- 空间复杂度:$O(1)$
思路2:哈希表
- 先查找字典中是否存在$target−nums[i]$,存在则输出 $target−nums[i]$ 对应的下标和当前数组的下标 $i$
- 不存在则在字典中存入 $target-nums[i]$的下标 $i$
def twoSum(self, nums: List[int], target: int) -> List[int]:
numDict = dict()
for i in range(len(nums)):
if target-nums[i] in numDict:
return numDict[target-nums[i]], i
numDict[nums[i]] = i
return [0]- 时间复杂度:$(n)$,其中 n 是数组 $nums$ 的元素数量。
- 空间复杂度:$O(n)$
LeetCode刷题攻略
1. LeetCode前期准备
- 常考的数据结构:数组、字符串、链表、树(如二叉树) 等。
- 常考的算法:分治算法、贪心算法、穷举算法、回溯算法、动态规划 等。
- 【书籍】「算法(第 4 版)- 谢路云 译」
- 【书籍】「大话数据结构 - 程杰 著」
- 【书籍】「趣学算法 - 陈小玉 著」
- 【书籍】「算法图解 - 袁国忠 译」
- 【书籍】「算法竞赛入门经典(第 2 版) - 刘汝佳 著」
- 【书籍】「数据结构与算法分析 - 冯舜玺 译」
- 【书籍】「算法导论(原书第 3 版) - 殷建平 / 徐云 / 王刚 / 刘晓光 / 苏明 / 邹恒明 / 王宏志 译」
- 「算法通关手册」GitHub 地址:https://github.com/itcharge/LeetCode-Py
- 「算法通关手册」电子书网站地址:https://algo.itcharge.cn
2. LeetCode刷题顺序
- 刷题列表(GitHub 版)链接:点击打开「GitHub 版分类刷题列表」
- 刷题列表(网页版)链接:点击打开「网页版分类刷题列表」
说明:「LeetCode 面试最常考 100 题」、「LeetCode 面试最常考 200 题」是笔者根据「CodeTop 企业题库」按频度从高到低进行筛选,并且去除了一部分 LeetCode 上没有的题目和重复题目后得到的题目清单。
- 「LeetCode 面试最常考 100 题(GitHub 版)」链接:点击打开「LeetCode 面试最常考 100 题(GitHub 版)」
- 「LeetCode 面试最常考 200 题(GitHub 版)」链接:点击打开「LeetCode 面试最常考 200 题(GitHub 版)」
- 「LeetCode 面试最常考 100 题(网页版)」链接:点击打开「LeetCode 面试最常考 100 题(网页版)」
- 「LeetCode 面试最常考 200 题(网页版)」链接:点击打开「LeetCode 面试最常考 200 题(网页版)」
3. LeetCode刷题技巧
- 五分钟思考法
- 重复刷题
- 按专题分类刷题
- 写解题报告
- 坚持刷题
五分钟思考法
五分钟思考法:如果一道题如果 5 分钟之内有思路,就立即动手写代码解题。如果 5 分钟之后还没有思路,就直接去看题解。然后根据题解的思路,自己去实现代码。如果发现自己看了题解也无法实现代码,就认真阅读题解的代码,并理解代码的逻辑。
重复刷题
重复刷题:遇见不会的题,多刷几遍,不断加深理解。
按专题分类刷题
按专题分类刷题:按照不同专题分类刷题,既可以巩固刚学完的算法知识,还可以提高刷题效率。
写解题报告
写解题报告:如果能够用简介清晰的语言让别人听懂这道题目的思路,那就说明你真正理解了这道题的解法。
坚持刷题
坚持刷题:算法刷题没有捷径,只有不断的刷题、总结,再刷题,再总结。
参考资料
作者: UncleLLD 发表日期:2023 年 8 月 25 日